Corrección / reflexión del examen 3ª Evaluación

En rasgos generales, salí con buenas sensaciones del examen aún que no del todo convencido en haber hecho un buen trabajo ya que eran 5 ejercicios y dos de ellos no les llegue a hacer porque no sabía. Lo que quiere decir que no estudie lo suficiente o lo que estudio no me rindió. Y ahora que veo los dos ejercicios que no hice, quizás hubiese sabido hacerles puesto que no era tan complicado.

Primer ejercicio: Valía 3 puntos, yo me pondría 1,5 o 2.
Porque no se si los procedimientos fueron del todo correctos, como por ejemplo en el apartado b, yo únicamente puse que era o por ser una constante, y en realidad había que haber dicho su dominio para poder decir que era una constante.

Segundo ejercicio: Valía 2 puntos, y siendo sincero no creo que llegue a 1.
Puse solamente las fórmulas de ecuación tangente y sustituí sin calcular nada por lo que no me dio ningún resultado. 

Tercer ejercicio: Valía 4 puntos.
A pesar de que nos diese el dibujo ya hecho no conseguí hacerlo. Se trataba de un problema del tipo de optimización igual que el otro que no conseguí hacer. Fue culpa mía no saber hacerlo ni entenderlo. Pero a lo mejor, solo tal vez hubiese sido mas conveniente tener mas tiempo para estudiarlo junto con las integrales, ya que se dio pocos días antes del examen. 
Pero ahora que veo la corrección que el profesor nos ha dado, no hubiese sido tan complicado hacerle. Simplemente había que utilizar la fórmula del área del triángulo, establecer una relación entre r y b, y calcular el área. A partir de ahí hacer la derivada segunda del área y evaluarla en el resultado que nos a dado, o con la derivada primera, estudiar el signo.

Cuarto ejercicio: Sobre 4 puntos, yo creo que tendría 3 o algo menos.
Este ejercicio era el estudio completo de la función, que se componía de 6 partes. La primera es el dominio, esta la tengo bien entera. La siguiente parte es los puntos de corte con los ejes, el corte con el eje y lo expliqué bien que no existía, el corte con el eje x, solo puse que cortaba por x=1 y no que también por x=-1. En la continuidad y asíntotas, posiblemente sea la parte que peor tengo, ya que no supe hallar las asíntotas oblicuas y en las horizontales no hice los límites necesarios para averiguarlo. En la monotonía y extremos relativos, sinceramente no recuerdo lo que puse, por lo que esperaré a que el profesor me vuelva a entregar el examen para poder ver mas detenidamente si lo puse bien o no. La parte de convexidad y puntos de inflexión la tengo completada correctamente. y por último la gráfica es quizás la parte que mas dejo de desear puesto que no hice la tabla de valores, no aplique los máximos y mínimos que encontré y la hice un poco a mano alzada.

Quinto ejercicio: Valía 2 puntos.
Este es el otro ejercicio que no conseguí realizar correctamente puesto que no le practique lo suficiente este tipo de problemas de optimización. Pero era bien sencillo lo único que había que hacer es aplicar la regla de Barrow correctamente y resolverlo. 

Como conclusión final puede decir que este examen a sido posiblemente en el que mas he aprendido, y para el que mas he trabajado aún que no de frutos. espero mejorar para el siguiente. 

Examen para casa correspondiente a la 3ª evaluación

Como ya es costumbre, antes de cada examen de matemáticas, el profesor nos manda una serie de ejercicios a modo de examen, sobre los contenidos de los que nos examinamos. Estos ejercicios son del tipo a los que tendremos en el examen.
 Este examen le hemos tenido hoy, y a parte hemos corregido algunos ejercicios del correspondiente examen para casa. Aquí os voy a dejar los ejercicios tal y como les tenía antes de la corrección.

Practicas de derivadas e integrales

Buscando en Google la forma de corregir las derivadas e integrales que estaba practicando, me encontré con una página que nos puede ayudar mucho a la hora de practicar, y entender lo que hacemos. 

Esta página tiene una calculadora científica, trigonométrica y en la cual se pueden incluir fracciones y raíces de todo tipo. Puedes pedir que te calcule la derivada o la integral de cualquier función, y explica los pasos que ha seguido para llegar a ese resultado. También te dice si a aplicado algún tipo de regla como las que ya hemos visto en este blog como la Regla de la Cadena, o la de L'Hopital. Y debajo de toda esta explicación hace una representación de de la integral o derivada que se halla obtenido.

Aquí os dejo el enlace:

https://es.symbolab.com/solver/integral-calculator 

Os invito a que la probéis y practiquéis con ella.

Regla de Barrow

La regla de Barrow dice que la integral definida de una función continua f(x) en un intervalo cerrado [a, b] es igual a la diferencia entre los valores que toma una función primitiva G(x) de f(x), en los extremos de dicho intervalo.

En esta imagen podemos ver el tipo de notación que utilizamos en estos casos. Ahora voy a poneros una serie de ejemplos, tanto partiendo de una gráfica como de una función "escrita".

Cálculo de áreas de regiones planas

Conocemos de sobra cuales son los procedimiento para hallar el área de un polígono regular, pero con esto vamos a poder aplicarlo a muchos mas casos como Por ejemplo en la siguiente figura:

Como sabemos calcular el área de un rectángulo, tenemos que intentar cubrir el mayor espacio posible a base de triángulos. Por lo que al final se va a basar en aplicar limites. Una vez que calculemos los límites tendremos el área.

Propiedades de la integral inmediata

Vamos a ir poco a poco introduciéndonos en las integrales, por lo que comenzaremos con las integrales inmediatas puesto que son las mas sencillas. Estas integrales inmediatas únicamente hay que "darle la vuelta a las derivadas de la tabla de derivadas que ya publiqué anteriormente. 

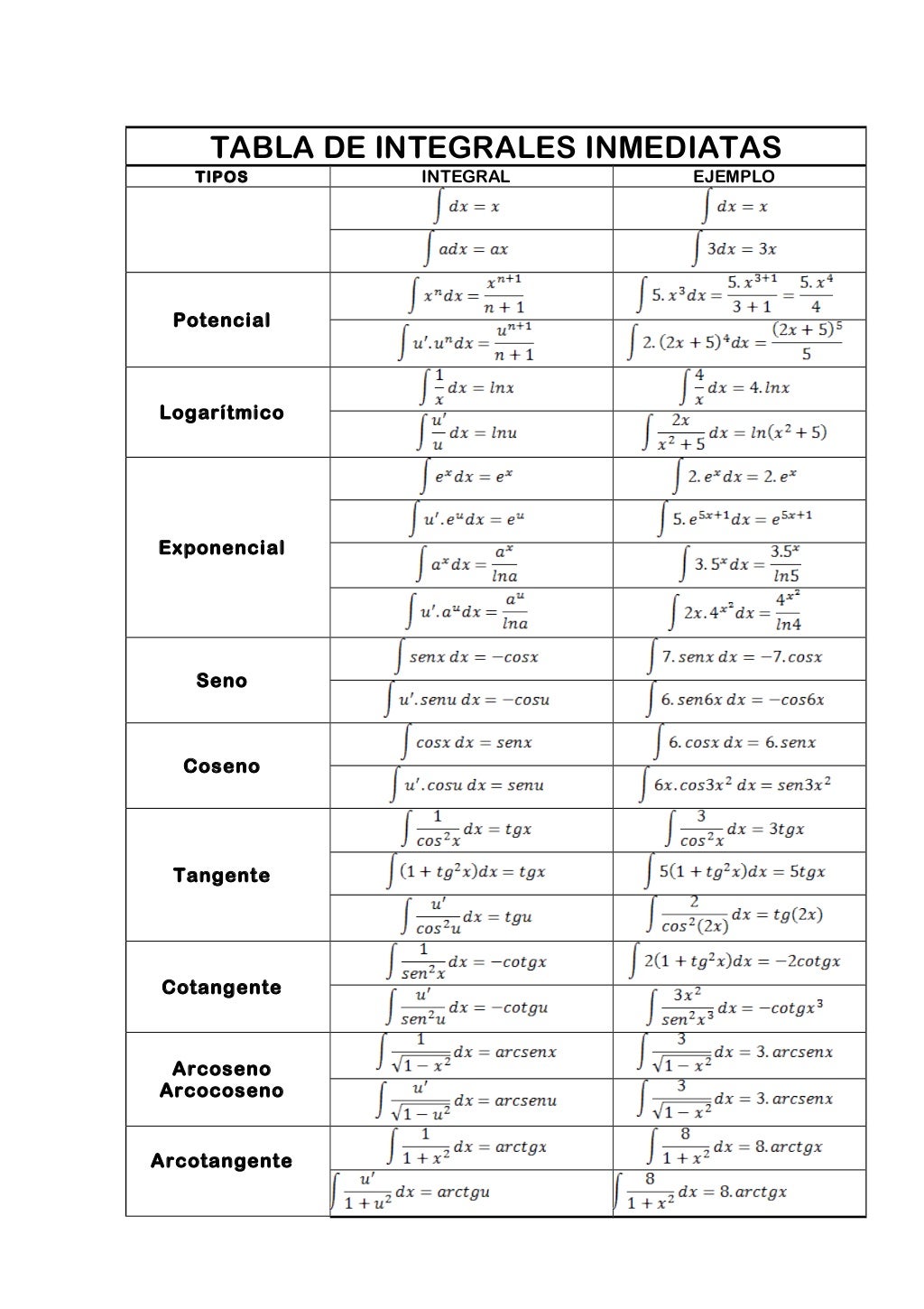
Pero antes de esto tenemos que conocer las propiedades de las integrales indefinidas: 

• La integral del producto de un número real por una función es igual al número real por la integral de la función.

• La integral de la suma (diferencia) de dos funciones es igual a la suma (diferencia) de las integrales de dichas funciones.

Ahora os voy a mostrar como se pueden ir haciendo los ejercicios mas simples, y a partir de algunos de estos sacaremos unas pequeñas reglas:

Primitiva de una función

Como ya hemos visto anteriormente, la derivación es una técnica que nos permite hallar la derivada de una función dada. Por ejemplo f(x)= X³ + 2, la derivada de esta función es f'(x)= 3x² . Ahora vamos a dar la vuelta a Esta correspondencia buscando cual será la función primitiva de esta función derivada. Este proceso es el que se conoce como integración. 

Cabe hacer un pequeño matiz a modo de observación, en el que diremos que una misma derivada tiene tantas funciones primitivas como se quiera. Y lo único que diferenciaría a estas funciones primitivas, seria la constante que se las va sumando.  
La notación que aplicaremos en estos casos de funciones primitivas es: