sábado, 31 de octubre de 2015
Teorema del resto
El resto de la división de un polinomio P(x), por ( x - a ) es el valor numerico de dicho polinomio para x = a.
domingo, 25 de octubre de 2015
Polinomios
En matemáticas es una relación de monomios o una sucesión de sumas y restas de potencias enteras de una o de varias variables indeterminadas.
El grado de un polinomio P(x) es el mayor exponente al que se encuentra elevada la variable x. Según su grado, los polinomios pueden ser:
Es aquel que se obtiene de sustituir la variable x por un número cualquiera.
P(x) = 2x3 + 5x2 - x + 1; para x = 1
P(1) = 2 · 13 + 5 ·12 - 1 + 1 = 7
El grado de un polinomio P(x) es el mayor exponente al que se encuentra elevada la variable x. Según su grado, los polinomios pueden ser:
- Primer grado: P(x) = 2x + 1,
- Segundo grado: P(x) = 2x2 - x + 1,
- Tercer grado: P(x) = 2x3 + 3x2 - x + 1,
- Polinomio nulo: Cuando todos sus coeficientes son nulos. P(x) = 0x + 0
- Polinomio completo: Cuando tiene todos los términos desde el independiente hasta el de mayor grado. P(x) = 2x3 + 3x2 - 4x + 1
- Polinomio incompleto: Aquel que no tiene todos los términos del polinomio. P(X) = 2x3 + 4x - 1
- Polinomio ordenado: Si los monomios que lo forman están ordenados de mayor a menor. P(x) = 2x3 + 3x2 - x + 1
Es aquel que se obtiene de sustituir la variable x por un número cualquiera.
P(x) = 2x3 + 5x2 - x + 1; para x = 1
P(1) = 2 · 13 + 5 ·12 - 1 + 1 = 7
Disputas matemáticas en el siglo XVI: Tartaglia, Cardano y del Ferro
Durante el siglo XVI tres grandes matemáticos enfocaron sus estudios hacia una parte de las matemáticas que hasta entonces estaba sin resolver. Esta parte eran las ecuaciones de ercer grado, ya se conocían las de segundo pero hasta entonces no hubo grandes avances. A parte de coincidir en el tiempo, también llegaron los tres a unas conclusiones muy parecidas sobre las ecuaciones de tercer grado.
Del Ferro fue el primero en resolver la ecuación, pero no se conservan muchos escritos sobre el y simplemente le comunicaba sus descubrimientos a su familia y alumnos. Tartaglia llego a las mismas conclusiones pero poco tiempo después, por lo que un alumno de del Ferro le reto a solucionar problemas de ecuaciones de tercer grado. Reto que Tartaglia gano ya que sabia resolver los dos tipos de ecuaciones de tercer grado. Y por último Cardano publico un libro con las formulas que resolvían estas ecuaciones, pero Cardano llego a saberlo gracias a que se lo dijo Tartaglia.
Me parece me parece que estas tres personas dieron un gran avance a las matemáticas de su siglo ya que todos ellos hicieron grandes descubrimientos. Y con respecto a la ecuación de tercer grado me sorprende como dos personas sin aparentemente nada que ver llegaron a las mismas conclusiones prácticamente en el mismo espacio de tiempo. Porque en mi opinión Cardano no llego a ninguna conclusión matemática de estas ecuaciones, si no que fue Tartaglia el que se lo dijo. Pero en realidad el primer matemático que llego a resolver estas ecuaciones fue del Ferro, pero únicamente de una forma, no como Tartaglia que lo logro de dos.
Aquí os dejo el link con las biografías de estos tres matemáticos y sus revueltas debido a esta ecuación:
http://historiaybiografias.com/disputas_matematicas/
Del Ferro fue el primero en resolver la ecuación, pero no se conservan muchos escritos sobre el y simplemente le comunicaba sus descubrimientos a su familia y alumnos. Tartaglia llego a las mismas conclusiones pero poco tiempo después, por lo que un alumno de del Ferro le reto a solucionar problemas de ecuaciones de tercer grado. Reto que Tartaglia gano ya que sabia resolver los dos tipos de ecuaciones de tercer grado. Y por último Cardano publico un libro con las formulas que resolvían estas ecuaciones, pero Cardano llego a saberlo gracias a que se lo dijo Tartaglia.
Me parece me parece que estas tres personas dieron un gran avance a las matemáticas de su siglo ya que todos ellos hicieron grandes descubrimientos. Y con respecto a la ecuación de tercer grado me sorprende como dos personas sin aparentemente nada que ver llegaron a las mismas conclusiones prácticamente en el mismo espacio de tiempo. Porque en mi opinión Cardano no llego a ninguna conclusión matemática de estas ecuaciones, si no que fue Tartaglia el que se lo dijo. Pero en realidad el primer matemático que llego a resolver estas ecuaciones fue del Ferro, pero únicamente de una forma, no como Tartaglia que lo logro de dos.
Aquí os dejo el link con las biografías de estos tres matemáticos y sus revueltas debido a esta ecuación:
http://historiaybiografias.com/disputas_matematicas/
jueves, 22 de octubre de 2015
Número Algebráico
Números reales que son solución de alguna ecuación polinómica cuyos coeficientes son números racionales.
Identidades notables relacionada con las ternas pitagóricas
Las ternas pitagóricas son un conjunto de números naturales que verifican:
x2 + y2 = z2
Es decir, que cumplen el teorema de Pitágoras.
Es decir, que cumplen el teorema de Pitágoras.
Ecuación diofántica
Se denomina ecuación diofántica a aquellas con dos o mas soluciones que son en ℤ, con soluciones enteras.
Un ejemplo de ecuación diofántica es:
Un ejemplo de ecuación diofántica es:
x+y= 5
Binomio de Newton
Una identidad notable es una multiplicación que cumple unas reglas fijas, como por ejemplo esta ecuación:
(a+b)2= a2 + 2ab +
b2
A través de la generalización de esta ecuación podemos llegar a lo que conocemos como binomio de Newton. Es una formula que nos permite calcular las potencias de un binomio.
lunes, 19 de octubre de 2015
Puede ser un numero radical racional?
Un numero radical es una expresión de la forma  en la que n
en la que n  ℚ y a
ℚ y a 
 ; con tal de que cuando n sea negativo, a a de ser impar.
; con tal de que cuando n sea negativo, a a de ser impar.
Ejemplo: x2 = 2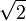 = X (
= X (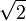 )2=2
)2=2
Respondiendo a la pregunta de que si todo numero radical puede ser acional, hay que responder que si. Porque tomando p cpmo un numero normal podemos ver: P ℚð P
ℚð P 

Pero nunca podriamos decir que P
 ð P
ð P  ℚ, ya que eso es falso, porque tambien existen los numeros irracionales entre los que se encuentran por ejemplo
ℚ, ya que eso es falso, porque tambien existen los numeros irracionales entre los que se encuentran por ejemplo  , e y muchos mas.
, e y muchos mas.
Ejemplo: x2 = 2
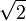 = X (
= X (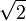 )2=2
)2=2Respondiendo a la pregunta de que si todo numero radical puede ser acional, hay que responder que si. Porque tomando p cpmo un numero normal podemos ver: P
Pero nunca podriamos decir que P
 , e y muchos mas.
, e y muchos mas.sábado, 17 de octubre de 2015
Leyes de De Morgan
1ª Ley de De Morgan:

2ª Ley de De Morgan:

Donde:
- ¬ es el operador de negación (NO)
 es el operador de conjunción (Y)
es el operador de conjunción (Y) es el operador de disyunción (O)
es el operador de disyunción (O)- ⇔ es una igualdad, es reciproco.
Como podemos observar, siempre que se niegan dos elementos al mismo tiempo con el operador "  ", se niegan por separado con el operador "
", se niegan por separado con el operador "  ". Y en la segunda ley ocurre lo mismo pero al contrario.
". Y en la segunda ley ocurre lo mismo pero al contrario.
 ", se niegan por separado con el operador "
", se niegan por separado con el operador "  ". Y en la segunda ley ocurre lo mismo pero al contrario.
". Y en la segunda ley ocurre lo mismo pero al contrario.
Suscribirse a:
Comentarios (Atom)


